意大利数学家裴波那契，在他所撰写的《Liber Abaci（算书）》一书，提出了著名的裴波那契数列。裴波那契数列旨在解决一个非常有趣的数学问题：即一对成年兔子平均每个月生一对小兔子，而一个月之后，小兔子成年也会加入生兔子的行列，如果每对兔子都经历这样出生、成熟、生育的过程，而且这些兔子永远不死的话， N个月之后将会有多少只兔子？这个问题用数列表示就是1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144……，而这个数列中的每一项就被称为裴波那契数。

著名天文学家开普勒，在1661年所著的《Strena seu de Nive Sexangula (六角雪花) 》一书中指出斐波那契数列在黄金分割数中收敛。黄金分割数实际上暗藏着很多的玄机无论是物理研究还是数学计算，总会在不知不觉当中就会冒出黄金分割数。

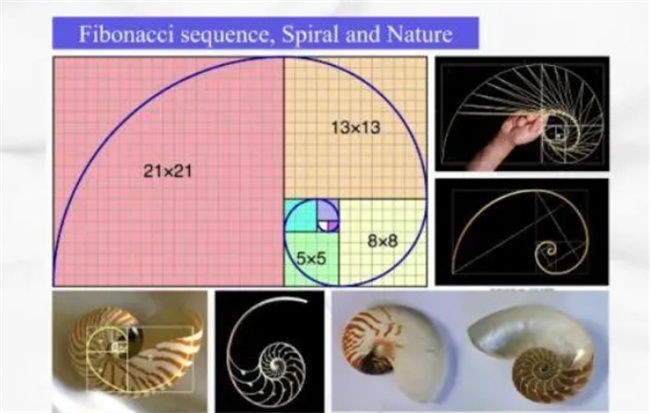
按照裴波那契数列，曲边长分别是1、1、2、3、5、8、13、21……的正方形，再将每个正方形的一个顶点当做圆心画出1/4的曲线，然后将所有的曲线连接在一起，最后就会形成螺旋线，这些螺旋线则被称为裴波那气旋线。